Дисертації з теми "Quantum random oracle model"

L'émergence des machines quantiques crée des défis et des opportunités pour la cryptographie. En particulier, les preuves de sécurité doivent être révisées en raison des capacités quantiques des adversaires. Cette thèse propose deux contributions à cet égard : un résultat positif et un résultat négatif. La transformation de Fiat-Shamir avec des rejets est l’un des principaux paradigmes pour concevoir des schémas de signature post-quantiques. Une partie de cette thèse consiste en une analyse détaillée de cette transformation dans le modèle de l’oracle aléatoire quantique. Tous les travaux précédents proposant une analyse de sécurité de cette transformation ont négligé des détails subtils, compromettant la correction des preuves. Par conséquent, notre preuve de sécurité est la première de son genre à être correcte. De plus, nous analysons le temps d'exécution et la correction des signatures obtenues à partir de cette transformation. Le problème learning with errors (LWE) a été largement utilisé pour construire des schémas cryptographiques sécurisés contre les adversaires quantiques. Une hypothèse liée à LWE stipule que la génération d'une instance LWE sans connaître son secret est difficile pour tous les algorithmes polynomiaux. On peut utiliser cette hypothèse pour prouver la sécurité de certains arguments de connaissance succints. Bien que cela semble être une tâche difficile pour les algorithmes classiques, nous présentons un algorithme quantique polynomial qui génère des instances LWE sans connaître le secret. Notre algorithme invalide ainsi les analyses de sécurité de ces arguments de connaissance succints dans le contexte quantique
The rise of quantum machines poses both challenges and opportunities for cryptography. In particular, security proofs may require revisions due to adversaries' quantum capabilities. This thesis presents two contributions in this respect: a positive result and a negative one. The Fiat-Shamir transform with aborts is one of the major paradigms for designing post-quantum secure signature schemes. Part of this thesis consists of a detailed security analysis of this transform in the quantum random oracle model. It is worth noting that all previous works have neglected subtle details, jeopardizing the correctness of their proofs. Consequently, our security proof stands as the first of its kind that is correct. Moreover, we analyze the runtime and correctness of the signatures obtained from this transform. The learning with errors (LWE) problem has been extensively utilized to construct cryptographic schemes that are secure against quantum adversaries. A knowledge assumption of the LWE problem states that obliviously sampling an LWE instance, namely without knowing its underlying secret, is hard for all polynomial-time algorithms. One can use this assumption to prove the security of some succinct non-interactive arguments of knowledge (SNARKs). While it seems a hard task for classical algorithms, we demonstrate a quantum polynomial-time oblivious LWE sampler. Consequently, our sampler breaks the security analysis of the mentioned SNARKs in the quantum setting

Over the years, people have found Quantum Mechanics to be extremely useful in explaining various physical phenomena from a microscopic point of view. Anderson localization, named after physicist P. W. Anderson, states that disorder in a crystal can cause non-spreading of wave packets, which is one possible mechanism (at single electron level) to explain metalinsulator transitions. The theory of quantum computation promises to bring greater computational power over classical computers by making use of some special features of Quantum Mechanics. The first part of this dissertation considers a 3D alloy-type model, where the Hamiltonian is the sum of the finite difference Laplacian corresponding to free motion of an electron and a random potential generated by a sign-indefinite single-site potential. The result shows that localization occurs in the weak disorder regime, i.e., when the coupling parameter λ is very small, for energies E ≤ −Cλ² . The second part of this dissertation considers adiabatic quantum computing (AQC) algorithms for the unstructured search problem to the case when the number of marked items is unknown. In an ideal situation, an explicit quantum algorithm together with a counting subroutine are given that achieve the optimal Grover speedup over classical algorithms, i.e., roughly speaking, reduce O(2n ) to O(2n/2 ), where n is the size of the problem. However, if one considers more realistic settings, the result shows this quantum speedup is achievable only under a very rigid control precision requirement (e.g., exponentially small control error).
Ph. D.

HTML clipboard Statistical physics seeks to explain macroscopic properties of matter in terms of microscopic interactions. Of particular interest is the phenomenon of phase transition: the sudden changes in macroscopic properties as external conditions are varied. Two models in particular are of great interest to mathematicians, namely the Ising model of a magnet and the percolation model of a porous solid. These models in turn are part of the unifying framework of the random-cluster representation, a model for random graphs which was first studied by Fortuin and Kasteleyn in the 1970’s. The random-cluster representation has proved extremely useful in proving important facts about the Ising model and similar models. In this work we study the corresponding graphical framework for two related models. The first model is the transverse field quantum Ising model, an extension of the original Ising model which was introduced by Lieb, Schultz and Mattis in the 1960’s. The second model is the space–time percolation process, which is closely related to the contact model for the spread of disease. In Chapter 2 we define the appropriate space–time random-cluster model and explore a range of useful probabilistic techniques for studying it. The space– time Potts model emerges as a natural generalization of the quantum Ising model. The basic properties of the phase transitions in these models are treated in this chapter, such as the fact that there is at most one unbounded fk-cluster, and the resulting lower bound on the critical value in . 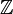In Chapter 3 we develop an alternative graphical representation of the quantum Ising model, called the random-parity representation. This representation is based on the random-current representation of the classical Ising model, and allows us to study in much greater detail the phase transition and critical behaviour. A major aim of this chapter is to prove sharpness of the phase transition in the quantum Ising model—a central issue in the theory— and to establish bounds on some critical exponents. We address these issues by using the random-parity representation to establish certain differential inequalities, integration of which gives the results. In Chapter 4 we explore some consequences and possible extensions of the results established in Chapters 2 and 3. For example, we determine the critical point for the quantum Ising model in 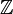and in ‘star-like’ geometries.
HTML clipboard Statistisk fysik syftar till att förklara ett materials makroskopiska egenskaper i termer av dess mikroskopiska struktur. En särskilt intressant egenskap är är fenomenet fasövergång, det vill säga en plötslig förändring i de makroskopiska egenskaperna när externa förutsättningar varieras. Två modeller är särskilt intressanta för en matematiker, nämligen Ising-modellen av en magnet och perkolationsmodellen av ett poröst material. Dessa två modeller sammanförs av den så-kallade fk-modellen, en slumpgrafsmodell som först studerades av Fortuin och Kasteleyn på 1970-talet. fk-modellen har sedermera visat sig vara extremt användbar för att bevisa viktiga resultat om Ising-modellen och liknande modeller. I den här avhandlingen studeras den motsvarande grafiska strukturen hos två näraliggande modeller. Den första av dessa är den kvantteoretiska Isingmodellen med transverst fält, vilken är en utveckling av den klassiska Isingmodellen och först studerades av Lieb, Schultz och Mattis på 1960-talet. Den andra modellen är rumtid-perkolation, som är nära besläktad med kontaktmodellen av infektionsspridning. I Kapitel 2 definieras rumtid-fk-modellen, och flera probabilistiska verktyg utforskas för att studera dess grundläggande egenskaper. Vi möter rumtid-Potts-modellen, som uppenbarar sig som en naturlig generalisering av den kvantteoretiska Ising-modellen. De viktigaste egenskaperna hos fasövergången i dessa modeller behandlas i detta kapitel, exempelvis det faktum att det i fk-modellen finns högst en obegränsad komponent, samt den undre gräns för det kritiska värdet som detta innebär. I Kapitel 3 utvecklas en alternativ grafisk framställning av den kvantteoretiska Ising-modellen, den så-kallade slumpparitetsframställningen. Denna är baserad på slumpflödesframställningen av den klassiska Ising-modellen, och är ett verktyg som låter oss studera fasövergången och gränsbeteendet mycket närmare. Huvudsyftet med detta kapitel är att bevisa att fasövergången är skarp—en central egenskap—samt att fastslå olikheter för vissa kritiska exponenter. Metoden består i att använda slumpparitetsframställningen för att härleda vissa differentialolikheter, vilka sedan kan integreras för att lägga fast att gränsen är skarp. I Kapitel 4 utforskas några konsekvenser, samt möjliga vidareutvecklingar, av resultaten i de tidigare kapitlen. Exempelvis bestäms det kritiska värdet hos den kvantteoretiska Ising-modellen på 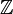, samt i ‘stjärnliknankde’ geometrier.
QC 20100705

Cette thèse explore divers aspects des cartes aléatoires par l'étude de trois modèles. Dans un premier temps, nous examinons les propriétés d’une mesure définie sur l’ensemble des triangulations de Delaunay planaires comportant n sommets, qui est un modèle de cartes où les arêtes sont décorées par des angles. Nous montrons ainsi que la mesure est égale à la mesure de Weil-Petersson sur l’espace des modules des surfaces de Riemann planaires marquées. Sont aussi montrées deux propriétés de la mesures, premiers pas d'une étude de la limite continue de ce modèle. Dans un deuxième temps, nous définissons des fonctions de corrélations sur les graphes de Strebel planaires isopérimétriques à n faces, qui sont des cartes métriques trivalentes. Les périmètres des faces sont fixés. Nous recourons au théorème de Kontsevich pour calculer les fonctions de corrélations en termes de nombres d’intersection de classes de Chern sur l’espace des modules des surfaces de Riemann. Pour la fonction à une face marquée, la limite des grandes cartes est examinée via l’approximation du point-selle, pour différents régimes du périmètre de la face marquée, et nous déduisons le régime où le comportement de la fonction de corrélation n’est pas trivial. Les fonctions de corrélations peuvent être calculées de manière systématique par la récurrence topologique. Partant, nous calculons la courbe spectrale de notre modèle, ce qui nous permet de montrer qu’il existe une courbe spectrale critique. Nous déduisons de cette courbe critique que la limite continue des graphes de Strebel isopérimétriques est un modèle minimal de type (3,2), habillé par la théorie de Liouville. Cela correspond bien à la gravité pure. Enfin, nous abordons la question des symétries dans le modèle d’Ising sur cartes aléatoires. Certaines fonctions de corrélations de ce modèle comptent le nombre de cartes bicolores avec des faces marquées, les bords, ayant des conditions aux bords mixtes, calculées par récurrence à partir de la courbe spectrale du modèle. Nous prouvons ici que, pour des courbes spectrales génériques, les fonctions de corrélations des cartes à un bord mixte sont symétriques par rotation et par inversion du bord mixte. Nous décrivons ensuite les conséquences de telles symétries, suggérant une possible reformulation du modèle en termes de chaînes de spins
This thesis explore several aspects of random maps through the study of three models. First, we examine the properties of a measure defined on the set of planar Delaunay triangulations with n vertices, a model in which the edges of the maps are decorated with angles. We show that the measure is the Weil-Petersson volume form on the moduli space of planar Riemann surfaces having n marked points. Two other properties, first steps toward the continuous limit study of the model, are also shown. Second, we define correlation functions on isoperimetric planar Strebel graphs with n faces, which are trivalent maps whose edges are decorated by positive lengths, and whose faces have a fixed perimeter. Kontsevich's theorem allows us to compute the correlation functions in terms of the intersection numbers of Chern classes of moduli space of Riemann surfaces. The continuous limit of the one-point function is computed in different regimes for the perimeter of the marked face via the saddle-point approximation. We identify the regime in which the behaviour of the one-point function is not trivial. The correlation functions can be computed in a systematic way by the Topological Recursion. To do so, we compute the spectral curve of the model, and show that there exists a critical spectral curve. We deduce from the latter that the continuous limit of isoperimetric Strebel graphs is a (3,2) minimal model dressed by Liouville theory: it corresponds to pure gravity. Last, we address the problem of symmetries in the Ising model on random maps. Some correlation functions of this model count the bi-colored maps with marked faces having mixed boundary conditions. They are computed via a recursive formula and the spectral curve of the model. We prove here that the correlation functions of maps with one mixed boundary, computed from the recursive relation with generic spectral curve, are invariant under rotation and inversion of the mixed boundary. We describe the consequences of such symmetries, suggesting a possible reformulation of the model in terms of spin chains

There are two types of vehicular communications: intra-vehicular and inter-vehicular. Widely used intra-vehicular communications protocols include Controller Area Network (CAN) 2.0B and Society of Automotive Engineers (SAE) J1939. Neither CAN 2.0B or SAE J1939 have included security mechanisms to prevent adversarial attacks. Adversaries may modify messages without detection. Inter-vehicular communications includes both vehicle-to-infrastructure and vehicle-to-vehicle communications. These are also vulnerable to attack. Manipulation of vehicular communications can have physical consequences endangering human life. This work aims to address this by analysing existing authentication protocols and designing secure authentication mechanisms for inter-vehicular and intra-vehicular communications to prevent certain adversarial attacks.

Denial-of-service (DoS) attacks are a growing concern to networked services like the Internet. In recent years, major Internet e-commerce and government sites have been disabled due to various DoS attacks. A common form of DoS attack is a resource depletion attack, in which an attacker tries to overload the server's resources, such as memory or computational power, rendering the server unable to service honest clients. A promising way to deal with this problem is for a defending server to identify and segregate malicious traffic as earlier as possible. Client puzzles, also known as proofs of work, have been shown to be a promising tool to thwart DoS attacks in network protocols, particularly in authentication protocols. In this thesis, we design efficient client puzzles and propose a stronger security model to analyse client puzzles. We revisit a few key establishment protocols to analyse their DoS resilient properties and strengthen them using existing and novel techniques. Our contributions in the thesis are manifold. We propose an efficient client puzzle that enjoys its security in the standard model under new computational assumptions. Assuming the presence of powerful DoS attackers, we find a weakness in the most recent security model proposed to analyse client puzzles and this study leads us to introduce a better security model for analysing client puzzles. We demonstrate the utility of our new security definitions by including two hash based stronger client puzzles. We also show that using stronger client puzzles any protocol can be converted into a provably secure DoS resilient key exchange protocol. In other contributions, we analyse DoS resilient properties of network protocols such as Just Fast Keying (JFK) and Transport Layer Security (TLS). In the JFK protocol, we identify a new DoS attack by applying Meadows' cost based framework to analyse DoS resilient properties. We also prove that the original security claim of JFK does not hold. Then we combine an existing technique to reduce the server cost and prove that the new variant of JFK achieves perfect forward secrecy (the property not achieved by original JFK protocol) and secure under the original security assumptions of JFK. Finally, we introduce a novel cost shifting technique which reduces the computation cost of the server significantly and employ the technique in the most important network protocol, TLS, to analyse the security of the resultant protocol. We also observe that the cost shifting technique can be incorporated in any Diffine{Hellman based key exchange protocol to reduce the Diffie{Hellman exponential cost of a party by one multiplication and one addition.

The dissertation covers phase transitions in the realm of the Anderson model of localization on topologically disordered Voronoi-Delaunay lattices. The disorder is given by random connections which implies correlations due to the restrictive lattice construction. Strictly speaking, the system features "strong anticorrelation", which is responsible for quenched long-range fluctuations of the coordination number. This attribute leads to violations of universal behavior in various system, e.g. Ising and Potts model, and to modifications of the Harris and the Imry-Ma criteria. In general, these exceptions serve to further understanding of critical phenomena. Hence, the question arises whether such deviations also occur in the realm of the Anderson model of localization in combination with random Voronoi-Delaunay lattice. For this purpose, four cases, which are distinguished by the spatial dimension of the systems and by the presence or absence of a magnetic field, are investigated by means of two different methods, i.e the multifractal analysis and the recursive Green function approach. The behavior is classified by the existence and type of occurring phase transitions and by the critical exponent v of the localization length. The results for the four cases can be summarized as follows. In two-dimensional systems, no phase transitions occur without a magnetic field, and all states are localized as a result of topological disorder. The behavior changes under the influence of the magnetic field. There are so-called quantum Hall transitions, which are phase changes between two localized regions. For low magnetic field strengths, the resulting exponent v ≈ 2.6 coincides with established values in literature. For higher strengths, an increased value, v ≈ 2.9, was determined. The deviations are probably caused by so-called Landau level coupling, where electrons scatter between different Landau levels. In contrast, the principle behavior in three-dimensional systems is equal in both cases. Two localization-delocalization transitions occur in each system. For these transitions the exponents v ≈ 1.58 and v ≈ 1.45 were determined for systems in absence and in presence of a magnetic field, respectively. This behavior and the obtained values agree with known results, and thus no deviation from the universal behavior can be observed
Diese Dissertation behandelt Phasenübergange im Rahmen des Anderson-Modells der Lokalisierung in topologisch ungeordneten Voronoi-Delaunay-Gittern. Die spezielle Art der Unordnung spiegelt sich u.a. in zufälligen Verknüpfungen wider, welche aufgrund der restriktiven Gitterkonstruktion miteinander korrelieren. Genauer gesagt zeigt das System eine "starke Antikorrelation", die dafür sorgt, dass langreichweitige Fluktuationen der Verknüpfungszahl unterdrückt werden. Diese Eigenschaft hat in anderen Systemen, z.B. im Ising- und Potts-Modell, zur Abweichung vom universellen Verhalten von Phasenübergängen geführt und bewirkt eine Modifikation von allgemeinen Aussagen, wie dem Harris- and Imry-Ma-Kriterium. Die Untersuchung solcher Ausnahmen dient zur Weiterentwicklung des Verständnisses von kritischen Phänomenen. Somit stellt sich die Frage, ob solche Abweichungen auch im Anderson-Modell der Lokalisierung unter Verwendung eines solchen Gitters auftreten. Dafür werden insgesamt vier Fälle, welche durch die Dimension des Gitters und durch die An- bzw. Abwesenheit eines magnetischen Feldes unterschieden werden, mit Hilfe zweier unterschiedlicher Methoden, d.h. der Multifraktalanalyse und der rekursiven Greensfunktionsmethode, untersucht. Das Verhalten wird anhand der Existenz und Art der Phasenübergänge und anhand des kritischen Exponenten v der Lokalisierungslänge unterschieden. Für die vier Fälle lassen sich die Ergebnisse wie folgt zusammenfassen. In zweidimensionalen Systemen treten ohne Magnetfeld keine Phasenübergänge auf und alle Zustände sind infolge der topologischen Unordnung lokalisiert. Unter Einfluss des Magnetfeldes ändert sich das Verhalten. Es kommt zur Ausformung von Landau-Bändern mit sogenannten Quanten-Hall-Übergängen, bei denen ein Phasenwechsel zwischen zwei lokalisierten Bereichen auftritt. Für geringe Magnetfeldstärken stimmen die erzielten Ergebnisse mit den bekannten Exponenten v ≈ 2.6 überein. Allerdings wurde für stärkere magnetische Felder ein höherer Wert, v ≈ 2.9, ermittelt. Die Abweichungen gehen vermutlich auf die zugleich gestiegene Unordnungsstärke zurück, welche dafür sorgt, dass Elektronen zwischen verschiedenen Landau-Bändern streuen können und so nicht das kritische Verhalten eines reinen Quanten-Hall-Überganges repräsentieren. Im Gegensatz dazu ist das Verhalten in dreidimensionalen Systemen für beide Fälle ähnlich. Es treten in jedem System zwei Phasenübergänge zwischen lokalisierten und delokalisierten Bereichen auf. Für diese Übergänge wurde der Exponent v ≈ 1.58 ohne und v ≈ 1.45 unter Einfluss eines magnetischen Feldes ermittelt. Dieses Verhalten und die jeweils ermittelten Werte stimmen mit bekannten Ergebnissen überein. Eine Abweichung vom universellen Verhalten wird somit nicht beobachtet

The contributions of this thesis fall into three areas of certificateless cryptography. The first area is encryption, where we propose new constructions for both identity-based and certificateless cryptography. We construct an n-out-of- n group encryption scheme for identity-based cryptography that does not require any special means to generate the keys of the trusted authorities that are participating. We also introduce a new security definition for chosen ciphertext secure multi-key encryption. We prove that our construction is secure as long as at least one authority is uncompromised, and show that the existing constructions for chosen ciphertext security from identity-based encryption also hold in the group encryption case. We then consider certificateless encryption as the special case of 2-out-of-2 group encryption and give constructions for highly efficient certificateless schemes in the standard model. Among these is the first construction of a lattice-based certificateless encryption scheme. Our next contribution is a highly efficient certificateless key encapsulation mechanism (KEM), that we prove secure in the standard model. We introduce a new way of proving the security of certificateless schemes based that are based on identity-based schemes. We leave the identity-based part of the proof intact, and just extend it to cover the part that is introduced by the certificateless scheme. We show that our construction is more efficient than any instanciation of generic constructions for certificateless key encapsulation in the standard model. The third area where the thesis contributes to the advancement of certificateless cryptography is key agreement. Swanson showed that many certificateless key agreement schemes are insecure if considered in a reasonable security model. We propose the first provably secure certificateless key agreement schemes in the strongest model for certificateless key agreement. We extend Swanson's definition for certificateless key agreement and give more power to the adversary. Our new schemes are secure as long as each party has at least one uncompromised secret. Our first construction is in the random oracle model and gives the adversary slightly more capabilities than our second construction in the standard model. Interestingly, our standard model construction is as efficient as the random oracle model construction.

Proving security of cryptographic schemes, which normally are short algorithms, has been known to be time-consuming and easy to get wrong. Using computers to analyse their security can help to solve the problem. This thesis focuses on methods of using computers to verify security of such schemes in cryptographic models. The contributions of this thesis to automated security proofs of cryptographic schemes can be divided into two groups: indirect and direct techniques. Regarding indirect ones, we propose a technique to verify the security of public-key-based key exchange protocols. Security of such protocols has been able to be proved automatically using an existing tool, but in a noncryptographic model. We show that under some conditions, security in that non-cryptographic model implies security in a common cryptographic one, the Bellare-Rogaway model [11]. The implication enables one to use that existing tool, which was designed to work with a different type of model, in order to achieve security proofs of public-key-based key exchange protocols in a cryptographic model. For direct techniques, we have two contributions. The first is a tool to verify Diffie-Hellmanbased key exchange protocols. In that work, we design a simple programming language for specifying Diffie-Hellman-based key exchange algorithms. The language has a semantics based on a cryptographic model, the Bellare-Rogaway model [11]. From the semantics, we build a Hoare-style logic which allows us to reason about the security of a key exchange algorithm, specified as a pair of initiator and responder programs. The other contribution to the direct technique line is on automated proofs for computational indistinguishability. Unlike the two other contributions, this one does not treat a fixed class of protocols. We construct a generic formalism which allows one to model the security problem of a variety of classes of cryptographic schemes as the indistinguishability between two pieces of information. We also design and implement an algorithm for solving indistinguishability problems. Compared to the two other works, this one covers significantly more types of schemes, but consequently, it can verify only weaker forms of security.

This thesis explores the theoretical representation of localised electrons in magnetic systems, using Majorana fermions. A motivation is provided for the Majorana fermion representation, which is then developed and applied as a mean-field theory and in the path-integral formalism to the Ising model in transversal-field (TFIM) in one, two and three dimensions, on an orthonormal lattice. In one dimension the development of domain walls precludes long-range order in discrete systems; this is as free energy savings due to entropy outweigh the energetic cost of a domain wall. An argument due to Peierls exists in 2D which allows the formation of domains of ordered spins amidst a disordered background, however, which may be extended to 3D. The forms of the couplings to the bosons used in the Random Phase Analysis (RPA) are considered and an explanation for the non-existence of the phases calculated in this thesis is discussed, in terms of spare degrees of freedom in the Majorana representation. This thesis contains the first known application of Majorana fermions at the RPA level.

A group key exchange (GKE) protocol allows a set of parties to agree upon a common secret session key over a public network. In this thesis, we focus on designing efficient GKE protocols using public key techniques and appropriately revising security models for GKE protocols. For the purpose of modelling and analysing the security of GKE protocols we apply the widely accepted computational complexity approach. The contributions of the thesis to the area of GKE protocols are manifold. We propose the first GKE protocol that requires only one round of communication and is proven secure in the standard model. Our protocol is generically constructed from a key encapsulation mechanism (KEM). We also suggest an efficient KEM from the literature, which satisfies the underlying security notion, to instantiate the generic protocol. We then concentrate on enhancing the security of one-round GKE protocols. A new model of security for forward secure GKE protocols is introduced and a generic one-round GKE protocol with forward security is then presented. The security of this protocol is also proven in the standard model. We also propose an efficient forward secure encryption scheme that can be used to instantiate the generic GKE protocol. Our next contributions are to the security models of GKE protocols. We observe that the analysis of GKE protocols has not been as extensive as that of two-party key exchange protocols. Particularly, the security attribute of key compromise impersonation (KCI) resilience has so far been ignored for GKE protocols. We model the security of GKE protocols addressing KCI attacks by both outsider and insider adversaries. We then show that a few existing protocols are not secure against KCI attacks. A new proof of security for an existing GKE protocol is given under the revised model assuming random oracles. Subsequently, we treat the security of GKE protocols in the universal composability (UC) framework. We present a new UC ideal functionality for GKE protocols capturing the security attribute of contributiveness. An existing protocol with minor revisions is then shown to realize our functionality in the random oracle model. Finally, we explore the possibility of constructing GKE protocols in the attribute-based setting. We introduce the concept of attribute-based group key exchange (AB-GKE). A security model for AB-GKE and a one-round AB-GKE protocol satisfying our security notion are presented. The protocol is generically constructed from a new cryptographic primitive called encapsulation policy attribute-based KEM (EP-AB-KEM), which we introduce in this thesis. We also present a new EP-AB-KEM with a proof of security assuming generic groups and random oracles. The EP-AB-KEM can be used to instantiate our generic AB-GKE protocol.

Mon travail de thèse est consacré à l’étude de quelques aspects de la physique quantique des systèmes quantiques à N corps en interaction. Il est orienté vers l’étude des chaînes de spins quantiques. Je me suis intéressé à plusieurs questions relatives aux chaînes de spins quantiques, du point de vue numérique et analytique à la fois. J'aborde en particulier les questions relatives à la structure des fonctions d'onde, la forme de la densité d'états et les propriétés spectrales des Hamiltoniens de chaînes de spins. Dans un premier temps, je présenterais très rapidement les techniques numériques de base pour le calcul des vecteurs et valeurs propres des Hamiltonien de chaînes de spins. Les densités d’états des modèles quantiques constituent des quantités importantes et très simples qui permettent de caractériser les propriétés spectrales des systèmes avec un grand nombre de degrés de liberté. Alors que dans la limite thermodynamique, les densités d'états de la plupart des modèles intégrables sont bien décrites par une loi gaussienne, dans certaines limites de couplage de la chaîne de spins au champ magnétique et pour un nombre de spins N fini sur la chaîne, on observe l’apparition de pics dans la densité d’états. Je montrerais que la connaissance des deux premiers moments du Hamiltonien dans le sous-espace dégénéré associé à chaque pics donne une bonne approximation de la densité d’états. Dans un deuxième temps je m'intéresserais aux propriétés spectrales des Hamiltoniens de chaînes de spins quantiques. L’un des principal résultats sur la statistique spectrale des systèmes quantiques concerne le comportement universel des fluctuations des mesures telles que l’espacement entre valeurs propres consécutives. Ces fluctuations sont bien décrites par la théorie des matrices aléatoires mais la comparaison avec les prédictions de cette théorie nécessite généralement une opération sur le spectre du Hamiltonien appelée unfolding. Dans les problèmes quantiques de N corps, la taille de l’espace de Hilbert croît généralement exponentiellement avec le nombre de particules, entraînant un manque de données pour pouvoir faire une statistique. Ces limitations ont amené l’introduction d’une nouvelle mesure se passant de la procédure d’unfolding basée sur le rapport d’espacements successifs plutôt que les espacements. En suivant l’idée du “surmise” de Wigner pour le calcul de la distribution de l’espacement, je montre comment calculer une approximation de la distribution du rapport d’espacements dans les trois ensembles gaussiens invariants en faisant le calcul pour des matrices 3x3. Les résultats obtenus pour les différents ensembles de matrices aléatoires se sont révélés être en excellent accord avec les résultats numériques. Enfin je m’intéresserais à la structure des fonctions d’ondes fondamentales des modèles de chaînes de spins quantiques. Les fonctions d’onde constituent, avec le spectre en énergie, les objets fondamentaux des systèmes quantiques : leur structure est assez compliquée et n’est pas très bien comprise pour la plupart des systèmes à N corps. En raison de la croissance exponentielle de la taille de l’espace de Hilbert avec le nombre de particules, l’étude des vecteurs propres est une tâche très difficile, non seulement du point de vue analytique mais aussi du point de vue numérique. Je démontrerais en particulier que l’état fondamental de tous les modèles que nous avons étudiés est multifractal avec en général une dimension fractale non triviale
My thesis is devoted to the study of some aspects of many body quantum interacting systems. In particular we focus on quantum spin chains. I have studied several aspects of quantum spin chains, from both numerical and analytical perspectives. I addressed especially questions related to the structure of eigenfunctions, the level densities and the spectral properties of spin chain Hamiltonians. In this thesis, I first present the basic numerical techniques used for the computation of eigenvalues and eigenvectors of spin chain Hamiltonians. Level densities of quantum models are important and simple quantities that allow to characterize spectral properties of systems with large number of degrees of freedom. It is well known that the level densities of most integrable models tend to the Gaussian in the thermodynamic limit. However, it appears that in certain limits of coupling of the spin chain to the magnetic field and for finite number of spins on the chain, one observes peaks in the level density. I will show that the knowledge of the first two moments of the Hamiltonian in the degenerate subspace associated with each peak give a good approximation to the level density. Next, I study the statistical properties of the eigenvalues of spin chain Hamiltonians. One of the main achievements in the study of the spectral statistics of quantum complex systems concerns the universal behaviour of the fluctuation of measure such as the distribution of spacing between two consecutive eigenvalues. These fluctuations are very well described by the theory of random matrices but the comparison with the theoretical prediction generally requires a transformation of the spectrum of the Hamiltonian called the unfolding procedure. For many-body quantum systems, the size of the Hilbert space generally grows exponentially with the number of particles leading to a lack of data to make a proper statistical study. These constraints have led to the introduction of a new measure free of the unfolding procedure and based on the ratio of consecutive level spacings rather than the spacings themselves. This measure is independant of the local level density. By following the Wigner surmise for the computation of the level spacing distribution, I obtained approximation for the distribution of the ratio of consecutive level spacings by analyzing random 3x3 matrices for the three canonical ensembles. The prediction are compared with numerical results showing excellent agreement. Finally, I investigate eigenfunction statistics of some canonical spin-chain Hamiltonians. Eigenfunctions together with the energy spectrum are the fundamental objects of quantum systems: their structure is quite complicated and not well understood. Due to the exponential growth of the size of the Hilbert space, the study of eigenfunctions is a very difficult task from both analytical and numerical points of view. I demonstrate that the groundstate eigenfunctions of all canonical models of spin chain are multifractal, by computing numerically the Rényi entropy and extrapolating it to obtain the multifractal dimensions

À partir des observations Z(n) = {(Xi, Yi), i = 1, ..., n} satisfaisant Yi = f(Xi) + ζi, nous voulons reconstruire la fonction f. Nous évaluons la qualité d'estimation par deux critères : le risque Ls et le risque uniforme. Dans ces deux cas, les hypothèses imposées sur la distribution du bruit ζi serons de moment borné et de type sous-gaussien respectivement. En proposant une collection des estimateurs à noyau, nous construisons une procédure, qui est initié par Goldenshluger et Lepski, pour choisir l'estimateur dans cette collection, sans aucune condition sur f. Nous prouvons ensuite que cet estimateur satisfait une inégalité d'oracle, qui nous permet d'obtenir les estimations minimax et minimax adaptatives sur les classes de Hölder anisotropes
From the observation Z(n) = {(Xi, Yi), i = 1, ..., n} satisfying Yi = f(Xi) + ζi, we would like to approximate the function f. This problem will be considered in two cases of loss function, Ls-risk and uniform risk, where the condition imposed on the distribution of the noise ζi is of bounded moment and of type sub-gaussian, respectively. From a proposed family of kernel estimators, we construct a procedure, which is initialized by Goldenshluger and Lepski, to choose in this family a final estimator, with no any assumption imposed on f. Then, we show that this estimator satisfies an oracle inequality which implies the minimax and minimax adaptive estimation over the anisotropic Hölder classes

Availability has become a primary goal of information security and is as significant as other goals, in particular, confidentiality and integrity. Maintaining availability of essential services on the public Internet is an increasingly difficult task in the presence of sophisticated attackers. Attackers may abuse limited computational resources of a service provider and thus managing computational costs is a key strategy for achieving the goal of availability. In this thesis we focus on cryptographic approaches for managing computational costs, in particular computational effort. We focus on two cryptographic techniques: computational puzzles in cryptographic protocols and secure outsourcing of cryptographic computations. This thesis contributes to the area of cryptographic protocols in the following ways. First we propose the most efficient puzzle scheme based on modular exponentiations which, unlike previous schemes of the same type, involves only a few modular multiplications for solution verification; our scheme is provably secure. We then introduce a new efficient gradual authentication protocol by integrating a puzzle into a specific signature scheme. Our software implementation results for the new authentication protocol show that our approach is more efficient and effective than the traditional RSA signature-based one and improves the DoSresilience of Secure Socket Layer (SSL) protocol, the most widely used security protocol on the Internet. Our next contributions are related to capturing a specific property that enables secure outsourcing of cryptographic tasks in partial-decryption. We formally define the property of (non-trivial) public verifiability for general encryption schemes, key encapsulation mechanisms (KEMs), and hybrid encryption schemes, encompassing public-key, identity-based, and tag-based encryption avors. We show that some generic transformations and concrete constructions enjoy this property and then present a new public-key encryption (PKE) scheme having this property and proof of security under the standard assumptions. Finally, we combine puzzles with PKE schemes for enabling delayed decryption in applications such as e-auctions and e-voting. For this we first introduce the notion of effort-release PKE (ER-PKE), encompassing the well-known timedrelease encryption and encapsulated key escrow techniques. We then present a security model for ER-PKE and a generic construction of ER-PKE complying with our security notion.

Cette these etudie les diagrammes de phase et l'integrabilite de differents modeles de physique statistique classique et quantique. Plusieurs methodes numeriques sont employees ; en particulier, un critere fonctionnel pour decider de l'integrabilite est presente. Le document est organise en deux parties independantes qui sont fortement reliees par les modeles etudies. La premiere partie applique la simulation de monte carlo a des modeles a spins classiques, non integrables, pour confronter des resultats de simulation a des propositions analytiques, obtenues recemment par l'etude des relations d'inverses et du groupe de symetries de ces modeles. Nous determinons ainsi les diagrammes de phase d'un modele de potts chiral a six etats sur reseau carre et du modele de potts standard a trois etats sur reseau triangulaire avec interactions a deux et trois spins. La deuxieme partie etudie l'integrabilite de differents modeles en physique statistique. Par des methodes de la theorie des matrices aleatoires nous analysons les proprietes statistiques du spectre d'un operateur decrivant le modele (le hamiltonien ou une matrice de transfert). En utilisant les symetries connues de celui-ci, on peut operer une decomposition en sous-espaces stables de cet operateur. Nous developpons la methode par l'etude systematique d'une chaine quantique de hubbard avec un terme d'echange. Par la suite, nous l'appliquons pour la premiere fois aux matrices de transfert de modeles classiques (modele d'ising 2d, 3d, modele de potts, modele a huit vertex asymetrique)

Adaptive security embodies one of the strongest notions of security that allows an adversary to corrupt parties at any point during protocol execution and gain access to its internal state. Since it models reallife situations such as “hacking”, efficient adaptively-secure multiparty computation (MPC) protocols are desirable. Such protocols demand primitives such as zero knowledge (ZK), oblivious transfer (OT) and commitment schemes that are adaptively-secure as building blocks. Efficient realizations of these primitives have been found to be challenging, especially in the no erasure model. We make progress in this direction and provide efficient constructions that are Universally-Composable in the random oracle model. The study of efficient ZK protocols for non-algebraic statements has seen rapid progress in recent times, relying on the techniques from secure computation. Our primary contribution in ZK lies in constructing efficient constant round ZK protocols from garbled circuits that are adaptively-secure, with communication linear in the size of the statement. We begin by showing that the practically efficient ZK protocol of Jawurek et al. (CCS 2013) is adaptively-secure when the underlying OT satisfies a mild adaptive security guarantee. We gain adaptive security with little to no overhead over the static case. A conditional verification technique is then used to obtain a three-round adaptively secure zero-knowledge argument in the non-programmable non-observable random oracle model. We present the first round optimal framework for building adaptively-secure OT in the programmable random oracle (PRO) model, relying upon the framework of Peikert et al. (Crypto 2008). When instantiated with Decisional Diffie Hellman assumption, it incurs a minimal communication overhead of one bit string and computational overhead of 5 random oracle queries over its static counterpart, where is the security parameter. Additionally, we obtain a construction of adaptively-secure 1-out-of-N OT by extending the result of Naor et al. (Journal of Cryptology 2005) that transforms log N copies of 1-out-of-2 OTs to one 1-out-of-N OT in the PRO model. We complete the picture of efficient OT constructions by presenting the first adaptively secure OT Extension, extending the protocol of Asharov et al. (Eurocrypt 2015) for the adaptive setting using PRO. Our OT extension enables us to obtain adaptive OTs at an amortized cost of 3 symmetric key operations and communication of 3 bit strings. We present an adaptively secure commitment scheme solely relying on observable random oracle (ORO). Our commitment scheme has a one-time offline setup phase, where a common reference string (crs) is generated between the parties using an ORO. In the online phase, the parties use the crs and ORO to generate commitments in a non-interactive fashion. Our construction incurs communication of 4 bit strings and computation of 8 exponentiations and 4 random oracle queries for committing to an arbitrary length message. It finds applications in secure two-party computation (2PC) protocols that adopt offline-online paradigm, where the crs can be generated in the offline phase and the scheme can be used in the online phase.

碩士
南華大學
資訊管理學系碩士班
97
A lot of designated verifier signature (DVS) schemes have been proposed. However, all of them only provide the basic security requirement that only the designated verifier can check the validity of the signature. They are either not secure enough or lacking source hiding. Hence, in this article, we design a provably secure DVS scheme. It not only can attain the basic security requirement but also hide the original signer''s identity which makes our scheme more suitable for the applications in an electronic voting system.

博士
國立臺灣大學
物理學研究所
90
Based on the framework of stochastic interpretation for quantum mechanics, two approaches are proposed to present several implications of quantum mechanics. One is the microscopic transport conservation approach for the random medium model. In this model, the quantum fluctuation of the microscopic object is assumed to arise from the collision between the microscopic object and the medion. Some assumptions for the object-medion collision are proposed to guarantee that the statistical ensemble manifestation of Schrodinger wave mechanics can be reproduced. According to this approach, several kinds of microscopic object energies and the local energy transport between the objects and the medions are studied. The other approach is the stochastic microscopic-phase-space formulation. A set of stochastic dynamic equations describing the motion of the individual object are proposed. According to this set of equations, a dynamic description for the von Neumann collapse is presented. Moreover, there exists the negativity of the microscopic-phase-space description in this formulation. The mechanism of the negativity is studied according to the stochastic dynamics. Some discussions on the significance of energy quantization and non-locality are also presented here.

Non-Interactive Key Agreement (NIKA) is a cryptographic primitive which allows two parties to agree on a shared secret key without any interaction. Identity-based Non-Interactive Key Agreement (ID-NIKA) allows each party to compute shared secret key using its own secret key and the peer’s identity. ID-NIKA can be used to establish shared secret keys in ad-hoc networks using minimal battery power and communication. Mobile Ad-hoc NETwork (MANET) is a network of mobile and moderately resource constrained devices communicating through a wireless medium. Examples of standard MANET devices are laptops, cellphones etc. Due to the inherent characteristics like mobility, dynamic topology and lack of centralized infrastructure, MANETs face some serious security issues. We are particularly interested about ID-NIKA in MANETs. This is of crucial interest for secure communication between two nodes in MANETs. In 2008, Gennaro et al. introduced a scheme called Hybrid Hierarchical Key Agreement Scheme (HH-KAS). HH-KAS uses subset based key agreement scheme at the non-leaf levels and a key agreement scheme due to Sakai et al. (referred as SOK-KAS) at the leaf level. HH-KAS is (i) non-interactive, (ii) identity-based, (iii) hierarchical and (iv) fully resilient against node compromises at leaf level and resilient against node compromises upto certain threshold values in non-leaf levels. Thus one can say that HH-KAS is partially resilient against node compromises. In their paper the authors claim that there is no key agreement scheme for MANETs in the literature, with all above four properties. This was motivated as an interesting open problem in this area. Guo et al. proposed a scheme known as Strong Key Agreement Scheme (SKAS) in 2011. The authors claimed it as a potential solution to the open problem posed by Gennaro et al. in their work. However, in 2014, Zhu et al. showed a concrete attack on SKAS. This attack makes SKAS practically useless for real life applications. Our main contribution is a hybrid scheme using two already existing schemes. Our scheme uses a deterministic key pre-distribution scheme by Lee and Stinson termed as Basic Id One-way function Scheme (BIOS) at level 1 (where root is at level 0). Beyond level 1, we use SOK-KAS for key agreement. We refer our scheme as BIOS-SOK key agreement. BIOS and SOK schemes satisfy properties (i), (ii) and (iv) but none of them is hierarchical in nature. In our work we have made an amalgam of both schemes which is hierarchical in nature. Thus, BIOS-SOK scheme satisfies (i), (ii), (iii) and is also fully resilient against arbitrary number of node compromises at any level. BIOS-SOK scheme also possesses the benefits of low space requirement, low shared key computation time and better scalability for many real-life applications when compared with the scheme of Gennaro et al. In HH-KAS, the key agreement is carried out only at the leaf level. In BIOS-SOK scheme, any two nodes in the hierarchy (at same or different levels) can compute shared secret key. We also provide a rigorous security analysis for our scheme in a stronger security model compared to the security model used for HH-KAS.
Indian Institute of Science

An identity-based cryptosystem (IBC) is a public-key system where the public key can be represented by any arbitrary string such as an e-mail address. The notion was introduced by Shamir with the primary goal of simplifying certificate management. An identity-based signature(IBS) is the identity-based counter part of a digital signature. In the first (and primary) part of the work, we take a closer look at an IBS due to Galindo and Garcia–GG-IBS, for short. GG-IBS is derived through a simple and elegant concatenation of two Schnorr signatures and, importantly, does not rely on pairing. The security is established through two algorithms (both of) which use the Multiple-Forking(MF) Algorithm to reduce the problem of computing the discrete logarithm to breaking the IBS. Our focus is on the security argument : It turns out that the argument is flawed and, as a remedy, we sketch a new security argument. However, the resulting security bound is still quite loose, chiefly due to the usage of the MF Algorithm. We explore possible avenues for improving this bound and , to this end, introduce two notions pertaining to random oracles termed dependency and independency. Incorporating (in) dependency allows us to launch the nested replay attack far more effectively than in the MF Algorithm leading to a cleaner,(significantly) tighter security argument for GG-IBS, completing the final piece of the GG-IBS jigsaw. The second part of the work pertains to the notion of selective-identity (sID) for IBCs. The focus is on the problem of constructing a fully-secure IBS given an sID-secure IBS without using random oracles and with reasonable security degradation.

An identity-based cryptosystem (IBC) is a public-key system where the public key can be represented by any arbitrary string such as an e-mail address. The notion was introduced by Shamir with the primary goal of simplifying certificate management. An identity-based signature(IBS) is the identity-based counter part of a digital signature. In the first (and primary) part of the work, we take a closer look at an IBS due to Galindo and Garcia–GG-IBS, for short. GG-IBS is derived through a simple and elegant concatenation of two Schnorr signatures and, importantly, does not rely on pairing. The security is established through two algorithms (both of) which use the Multiple-Forking(MF) Algorithm to reduce the problem of computing the discrete logarithm to breaking the IBS. Our focus is on the security argument : It turns out that the argument is flawed and, as a remedy, we sketch a new security argument. However, the resulting security bound is still quite loose, chiefly due to the usage of the MF Algorithm. We explore possible avenues for improving this bound and , to this end, introduce two notions pertaining to random oracles termed dependency and independency. Incorporating (in) dependency allows us to launch the nested replay attack far more effectively than in the MF Algorithm leading to a cleaner,(significantly) tighter security argument for GG-IBS, completing the final piece of the GG-IBS jigsaw. The second part of the work pertains to the notion of selective-identity (sID) for IBCs. The focus is on the problem of constructing a fully-secure IBS given an sID-secure IBS without using random oracles and with reasonable security degradation.

This thesis covers most of my work in the field of ultracold atoms loaded in optical lattices. This thesis can be divided into five different parts. In Chapter 1, after a brief introduction to the field of optical lattices I review the fundamental aspects pertaining to the physics of systems in periodic potentials and a short overview of the experiments on ultracold atoms in an optical lattice. In Chapter 2 we develop an inhomogeneous mean-field theory for the extended Bose-Hubbard model with a quadratic, confining potential. In the absence of this poten¬tial, our mean-field theory yields the phase diagram of the homogeneous extended Bose-Hubbard model. This phase diagram shows a superfluid (SF) phase and lobes of Mott-insulator(MI), density-wave(DW), and supersolid (SS) phases in the plane of the chemical potential and on-site repulsion ; we present phase diagrams for representative values of , the repulsive energy for bosons on nearest-neighbor sites. We demonstrate that, when the confining potential is present, superfluid and density-wave order parameters are nonuniform; in particular, we obtain, for a few representative values of parameters, spherical shells of SF, MI ,DW ,and SSphases. We explore the implications of our study for experiments on cold-atom dipolar con¬densates in optical lattices in a confining potential. In Chapter3 we present an extensive study of Mottinsulator( MI) and superfluid (SF) shells in Bose-Hubbard (BH) models for bosons in optical lattices with har¬monic traps. For this we develop an inhomogeneous mean-field theory. Our results for the BH model with one type of spinless bosons agrees quantitatively with quan¬tum Monte Carlo(QMC) simulations. Our approach is numerically less intensive than such simulations, so we are able to perform calculations on experimentally realistic, large three-dimensional(3D) systems, explore a wide range of parameter values, and make direct contact with a variety of experimental measurements. We also generalize our inhomogeneous mean-field theory to study BH models with har¬monic traps and(a) two species of bosons or(b) spin-1bosons. With two species of bosons we obtain rich phase diagrams with a variety of SF and MI phases and as¬sociated shells, when we include a quadratic confining potential. For the spin-1BH model we show, in a representative case, that the system can display alternating shells of polar SF and MI phases; and we make interesting predictions for experi¬ments in such systems. . In Chapter 4 we carry out an extensive study of the phase diagrams of the ex-tended Bose Hubbard model, with a mean filling of one boson per site, in one dimension by using the density matrix renormalization group and show that it contains Superfluid (SF), Mott-insulator (MI), density-wave (DW) and Haldane ¬insulator(HI) phases. We show that the critical exponents and central charge for the HI-DW,MI-HI and SF-MI transitions are consistent with those for models in the two-dimensional Ising, Gaussian, and Berezinskii-Kosterlitz-Thouless (BKT) uni¬versality classes, respectively; and we suggest that the SF-HI transition may be more exotic than a simple BKT transition. We show explicitly that different bound¬ary conditions lead to different phase diagrams.. In Chapter 5 we obtain the excitation spectra of the following three generalized of Bose-Hubbard(BH) models:(1) a two-species generalization of the spinless BH model, (2) a single-species, spin-1 BH model, and (3) the extended Bose-Hubbard model (EBH) for spinless interacting bosons of one species. In all the phases of these models we show how to obtain excitation spectra by using the random phase approximation (RPA). We compare the results of our work with earlier studies of related models and discuss implications for experiments.

This thesis covers most of my work in the field of ultracold atoms loaded in optical lattices. This thesis can be divided into five different parts. In Chapter 1, after a brief introduction to the field of optical lattices I review the fundamental aspects pertaining to the physics of systems in periodic potentials and a short overview of the experiments on ultracold atoms in an optical lattice. In Chapter 2 we develop an inhomogeneous mean-field theory for the extended Bose-Hubbard model with a quadratic, confining potential. In the absence of this poten¬tial, our mean-field theory yields the phase diagram of the homogeneous extended Bose-Hubbard model. This phase diagram shows a superfluid (SF) phase and lobes of Mott-insulator(MI), density-wave(DW), and supersolid (SS) phases in the plane of the chemical potential and on-site repulsion ; we present phase diagrams for representative values of , the repulsive energy for bosons on nearest-neighbor sites. We demonstrate that, when the confining potential is present, superfluid and density-wave order parameters are nonuniform; in particular, we obtain, for a few representative values of parameters, spherical shells of SF, MI ,DW ,and SSphases. We explore the implications of our study for experiments on cold-atom dipolar con¬densates in optical lattices in a confining potential. In Chapter3 we present an extensive study of Mottinsulator( MI) and superfluid (SF) shells in Bose-Hubbard (BH) models for bosons in optical lattices with har¬monic traps. For this we develop an inhomogeneous mean-field theory. Our results for the BH model with one type of spinless bosons agrees quantitatively with quan¬tum Monte Carlo(QMC) simulations. Our approach is numerically less intensive than such simulations, so we are able to perform calculations on experimentally realistic, large three-dimensional(3D) systems, explore a wide range of parameter values, and make direct contact with a variety of experimental measurements. We also generalize our inhomogeneous mean-field theory to study BH models with har¬monic traps and(a) two species of bosons or(b) spin-1bosons. With two species of bosons we obtain rich phase diagrams with a variety of SF and MI phases and as¬sociated shells, when we include a quadratic confining potential. For the spin-1BH model we show, in a representative case, that the system can display alternating shells of polar SF and MI phases; and we make interesting predictions for experi¬ments in such systems. . In Chapter 4 we carry out an extensive study of the phase diagrams of the ex-tended Bose Hubbard model, with a mean filling of one boson per site, in one dimension by using the density matrix renormalization group and show that it contains Superfluid (SF), Mott-insulator (MI), density-wave (DW) and Haldane ¬insulator(HI) phases. We show that the critical exponents and central charge for the HI-DW,MI-HI and SF-MI transitions are consistent with those for models in the two-dimensional Ising, Gaussian, and Berezinskii-Kosterlitz-Thouless (BKT) uni¬versality classes, respectively; and we suggest that the SF-HI transition may be more exotic than a simple BKT transition. We show explicitly that different bound¬ary conditions lead to different phase diagrams.. In Chapter 5 we obtain the excitation spectra of the following three generalized of Bose-Hubbard(BH) models:(1) a two-species generalization of the spinless BH model, (2) a single-species, spin-1 BH model, and (3) the extended Bose-Hubbard model (EBH) for spinless interacting bosons of one species. In all the phases of these models we show how to obtain excitation spectra by using the random phase approximation (RPA). We compare the results of our work with earlier studies of related models and discuss implications for experiments.