Relevant bibliographies by topics / Quantum random oracle model

Contents

  1. Journal articles
  2. Dissertations / Theses
  3. Books
  4. Book chapters
  5. Conference papers

Academic literature on the topic 'Quantum random oracle model'

Author: Grafiati
Published: 21 September 2024

Create a spot-on reference in APA, MLA, Chicago, Harvard, and other styles

Select a source type:

Consult the lists of relevant articles, books, theses, conference reports, and other scholarly sources on the topic 'Quantum random oracle model.'

Next to every source in the list of references, there is an 'Add to bibliography' button. Press on it, and we will generate automatically the bibliographic reference to the chosen work in the citation style you need: APA, MLA, Harvard, Chicago, Vancouver, etc.

You can also download the full text of the academic publication as pdf and read online its abstract whenever available in the metadata.

Journal articles on the topic "Quantum random oracle model"

1

Zhandry, Mark. "Secure identity-based encryption in the quantum random oracle model." International Journal of Quantum Information 13, no. 04 (June 2015): 1550014. http://dx.doi.org/10.1142/s0219749915500148.

Full text
Abstract:
We give the first proof of security for an identity-based encryption (IBE) scheme in the quantum random oracle model. This is the first proof of security for any scheme in this model that does not rely on the assumed existence of so-called quantum-secure pseudorandom functions (PRFs). Our techniques are quite general and we use them to obtain security proofs for two random oracle hierarchical IBE schemes and a random oracle signature scheme, all of which have previously resisted quantum security proofs, even assuming quantum-secure PRFs. We also explain how to remove quantum-secure PRFs from prior quantum random oracle model proofs. We accomplish these results by developing new tools for arguing that quantum algorithms cannot distinguish between two oracle distributions. Using a particular class of oracle distributions that we call semi-constant distributions, we argue that the aforementioned cryptosystems are secure against quantum adversaries.
APA, Harvard, Vancouver, ISO, and other styles
2

Shang, Tao, Ranyiliu Chen, and Qi Lei. "Quantum Random Oracle Model for Quantum Public-Key Encryption." IEEE Access 7 (2019): 130024–31. http://dx.doi.org/10.1109/access.2019.2940406.

Full text
APA, Harvard, Vancouver, ISO, and other styles
3

Harrow, Aram W., and David J. Rosenbaum. "Uselessness for an Oracle model with internal randomness." Quantum Information and Computation 14, no. 7&8 (May 2014): 608–24. http://dx.doi.org/10.26421/qic14.7-8-5.

Full text
Abstract:
We consider a generalization of the standard oracle model in which the oracle acts on the target with a permutation selected according to internal random coins. We describe several problems that are impossible to solve classically but can be solved by a quantum algorithm using a single query; we show that such infinity-vs-one separations between classical and quantum query complexities can be constructed from much weaker separations. We also give conditions to determine when oracle problems -- either in the standard model, or in any of the generalizations we consider -- cannot be solved with success probability better than random guessing would achieve. In the oracle model with internal randomness where the goal is to gain any nonzero advantage over guessing, we prove (roughly speaking) that k quantum queries are equivalent in power to 2k classical queries, thus extending results of Meyer and Pommersheim.
APA, Harvard, Vancouver, ISO, and other styles
4

Gama, Mariana, Paulo Mateus, and André Souto. "A Private Quantum Bit String Commitment." Entropy 22, no. 3 (February 27, 2020): 272. http://dx.doi.org/10.3390/e22030272.

Full text
Abstract:
We propose an entanglement-based quantum bit string commitment protocol whose composability is proven in the random oracle model. This protocol has the additional property of preserving the privacy of the committed message. Even though this property is not resilient against man-in-the-middle attacks, this threat can be circumvented by considering that the parties communicate through an authenticated channel. The protocol remains secure and private (but not composable) if we realize the random oracles as physical unclonable functions (PUFs) in the so-called bad PUF model.
APA, Harvard, Vancouver, ISO, and other styles
5

Goncalves, Brian, and Atefeh Mashatan. "Tightly Secure PKE Combiner in the Quantum Random Oracle Model." Cryptography 6, no. 2 (March 29, 2022): 15. http://dx.doi.org/10.3390/cryptography6020015.

Full text
Abstract:
The development of increasingly sophisticated quantum computers poses a long-term threat to current cryptographic infrastructure. This has spurred research into both quantum-resistant algorithms and how to safely transition real-world implementations and protocols to quantum-resistant replacements. This transition is likely to be a gradual process due to both the complexity and cost associated with transitioning. One method to ease the transition is the use of classical–quantum hybrid schemes, which provide security against both classical and quantum adversaries. We present a new combiner for creating hybrid encryption schemes directly from traditional encryption schemes. Our construction is the only existing proposal in the literature with IND-CCA-security in the classical and quantum random oracle models, respectively.
APA, Harvard, Vancouver, ISO, and other styles
6

Banegas, Gustavo, Paulo S. L. M. Barreto, Brice Odilon Boidje, Pierre-Louis Cayrel, Gilbert Ndollane Dione, Kris Gaj, Cheikh Thiécoumba Gueye, et al. "DAGS: Key encapsulation using dyadic GS codes." Journal of Mathematical Cryptology 12, no. 4 (December 1, 2018): 221–39. http://dx.doi.org/10.1515/jmc-2018-0027.

Full text
Abstract:
Abstract Code-based cryptography is one of the main areas of interest for NIST’s Post-Quantum Cryptography Standardization call. In this paper, we introduce DAGS, a Key Encapsulation Mechanism (KEM) based on quasi-dyadic generalized Srivastava codes. The scheme is proved to be IND-CCA secure in both random oracle model and quantum random oracle model. We believe that DAGS will offer competitive performance, especially when compared with other existing code-based schemes, and represent a valid candidate for post-quantum standardization.
APA, Harvard, Vancouver, ISO, and other styles
7

Chen, Lijie, and Ramis Movassagh. "Quantum Merkle Trees." Quantum 8 (June 18, 2024): 1380. http://dx.doi.org/10.22331/q-2024-06-18-1380.

Full text
Abstract:
Committing to information is a central task in cryptography, where a party (typically called a prover) stores a piece of information (e.g., a bit string) with the promise of not changing it. This information can be accessed by another party (typically called the verifier), who can later learn the information and verify that it was not meddled with. Merkle trees \cite{Merkle87} are a well-known construction for doing so in a succinct manner, in which the verifier can learn any part of the information by receiving a short proof from the honest prover. Despite its significance in classical cryptography, there was no quantum analog of the Merkle tree. A direct generalization using the Quantum Random Oracle Model (QROM) \cite{BonehDFLSZ11} does not seem to be secure. In this work, we propose the quantum Merkle tree. It is based on what we call the Quantum Haar Random Oracle Model (QHROM). In QHROM, both the prover and the verifier have access to a Haar random quantum oracle G and its inverse.Using the quantum Merkle tree, we propose a succinct quantum argument for the Gap-k-Local-Hamiltonian problem. Assuming the Quantum PCP conjecture is true, this succinct argument extends to all of QMA. This work raises a number of interesting open research problems.
APA, Harvard, Vancouver, ISO, and other styles
8

Kandii, S. O., and I. D. Gorbenko. "Analysis of DSTU 8961:2019 in the quantum random oracle model." Radiotekhnika, no. 214 (September 29, 2023): 7–16. http://dx.doi.org/10.30837/rt.2023.3.214.01.

Full text
Abstract:
Modern cryptographic transformations require provable security against a relatively wide class of threats. Typically, such evidentiary security is achieved through formal analysis within the chosen security model. The development of quantum computers led to the emergence of new attack vectors to which classical cryptography was vulnerable. However, there are cryptographic systems that are considered resistant to quantum attacks and some of them are even standardized. The formal analysis of such systems has faced difficulties for a long time, which were associated with the impossibility of applying classical methods of proof to formal models that take into account quantum effects. However, in recent years, many new results have appeared that allow obtaining formal security proofs for quite complex cryptographic transformations, and most of the existing post-quantum asymmetric encryption and key encapsulation schemes currently have corresponding formal proofs within the quantum random oracle model, the most widespread security model for of post-quantum cryptography. DSTU 8961:2019 is the Ukrainian post-quantum standard for asymmetric encryption and key encapsulation. However, security proofs in the quantum random oracle model have not yet been published for it. As part of this work, security evidence was obtained for the design of the key encapsulation mechanism described in DSTU 8961:209. The obtained result is generalized for an arbitrary asymmetric encryption scheme, which may contain decryption errors and can be used to assess the security of not only DSTU 8961:2019, but also other similar asymmetric transformations.
APA, Harvard, Vancouver, ISO, and other styles
9

Coladangelo, Andrea, Christian Majenz, and Alexander Poremba. "Quantum copy-protection of compute-and-compare programs in the quantum random oracle model." Quantum 8 (May 2, 2024): 1330. http://dx.doi.org/10.22331/q-2024-05-02-1330.

Full text
Abstract:
Copy-protection allows a software distributor to encode a program in such a way that it can be evaluated on any input, yet it cannot be "pirated" – a notion that is impossible to achieve in a classical setting. Aaronson (CCC 2009) initiated the formal study of quantum copy-protection schemes, and speculated that quantum cryptography could offer a solution to the problem thanks to the quantum no-cloning theorem. In this work, we introduce a quantum copy-protection scheme for a large class of evasive functions known as "compute-and-compare programs" – a more expressive generalization of point functions. A compute-and-compare program CC[f,y] is specified by a function f and a string y within its range: on input x, CC[f,y] outputs 1, if f(x)=y, and 0 otherwise. We prove that our scheme achieves non-trivial security against fully malicious adversaries in the quantum random oracle model (QROM), which makes it the first copy-protection scheme to enjoy any level of provable security in a standard cryptographic model. As a complementary result, we show that the same scheme fulfils a weaker notion of software protection, called "secure software leasing", introduced very recently by Ananth and La Placa (eprint 2020), with a standard security bound in the QROM, i.e. guaranteeing negligible adversarial advantage. Finally, as a third contribution, we elucidate the relationship between unclonable encryption and copy-protection for multi-bit output point functions.
APA, Harvard, Vancouver, ISO, and other styles
10

Yan, Jianhua, Licheng Wang, Lihua Wang, Yixian Yang, and Wenbin Yao. "Efficient Lattice-Based Signcryption in Standard Model." Mathematical Problems in Engineering 2013 (2013): 1–18. http://dx.doi.org/10.1155/2013/702539.

Full text
Abstract:
Signcryption is a cryptographic primitive that can perform digital signature and public encryption simultaneously at a significantly reduced cost. This advantage makes it highly useful in many applications. However, most existing signcryption schemes are seriously challenged by the booming of quantum computations. As an interesting stepping stone in the post-quantum cryptographic community, two lattice-based signcryption schemes were proposed recently. But both of them were merely proved to be secure in the random oracle models. Therefore, the main contribution of this paper is to propose a new lattice-based signcryption scheme that can be proved to be secure in the standard model.
APA, Harvard, Vancouver, ISO, and other styles
More sources

Dissertations / Theses on the topic "Quantum random oracle model"

1

Fallahpour, Pouria. "Lattice-based cryptography in a quantum setting : security proofs and attacks." Electronic Thesis or Diss., Lyon, École normale supérieure, 2024. http://www.theses.fr/2024ENSL0023.

Full text
Abstract:
L'émergence des machines quantiques crée des défis et des opportunités pour la cryptographie. En particulier, les preuves de sécurité doivent être révisées en raison des capacités quantiques des adversaires. Cette thèse propose deux contributions à cet égard : un résultat positif et un résultat négatif. La transformation de Fiat-Shamir avec des rejets est l’un des principaux paradigmes pour concevoir des schémas de signature post-quantiques. Une partie de cette thèse consiste en une analyse détaillée de cette transformation dans le modèle de l’oracle aléatoire quantique. Tous les travaux précédents proposant une analyse de sécurité de cette transformation ont négligé des détails subtils, compromettant la correction des preuves. Par conséquent, notre preuve de sécurité est la première de son genre à être correcte. De plus, nous analysons le temps d'exécution et la correction des signatures obtenues à partir de cette transformation. Le problème learning with errors (LWE) a été largement utilisé pour construire des schémas cryptographiques sécurisés contre les adversaires quantiques. Une hypothèse liée à LWE stipule que la génération d'une instance LWE sans connaître son secret est difficile pour tous les algorithmes polynomiaux. On peut utiliser cette hypothèse pour prouver la sécurité de certains arguments de connaissance succints. Bien que cela semble être une tâche difficile pour les algorithmes classiques, nous présentons un algorithme quantique polynomial qui génère des instances LWE sans connaître le secret. Notre algorithme invalide ainsi les analyses de sécurité de ces arguments de connaissance succints dans le contexte quantique
The rise of quantum machines poses both challenges and opportunities for cryptography. In particular, security proofs may require revisions due to adversaries' quantum capabilities. This thesis presents two contributions in this respect: a positive result and a negative one. The Fiat-Shamir transform with aborts is one of the major paradigms for designing post-quantum secure signature schemes. Part of this thesis consists of a detailed security analysis of this transform in the quantum random oracle model. It is worth noting that all previous works have neglected subtle details, jeopardizing the correctness of their proofs. Consequently, our security proof stands as the first of its kind that is correct. Moreover, we analyze the runtime and correctness of the signatures obtained from this transform. The learning with errors (LWE) problem has been extensively utilized to construct cryptographic schemes that are secure against quantum adversaries. A knowledge assumption of the LWE problem states that obliviously sampling an LWE instance, namely without knowing its underlying secret, is hard for all polynomial-time algorithms. One can use this assumption to prove the security of some succinct non-interactive arguments of knowledge (SNARKs). While it seems a hard task for classical algorithms, we demonstrate a quantum polynomial-time oblivious LWE sampler. Consequently, our sampler breaks the security analysis of the mentioned SNARKs in the quantum setting
APA, Harvard, Vancouver, ISO, and other styles
2

Aronsen, Kristoffer. "Quantum Criticality in the Transverse Field Random Ising Model." Thesis, KTH, Fysik, 2019. http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-257771.

Full text
APA, Harvard, Vancouver, ISO, and other styles
3

Cao, Zhenwei. "Quantum evolution: The case of weak localization for a 3D alloy-type Anderson model and application to Hamiltonian based quantum computation." Diss., Virginia Tech, 2012. http://hdl.handle.net/10919/19205.

Full text
Abstract:
Over the years, people have found Quantum Mechanics to be extremely useful in explaining various physical phenomena from a microscopic point of view. Anderson localization, named after physicist P. W. Anderson, states that disorder in a crystal can cause non-spreading of wave packets, which is one possible mechanism (at single electron level) to explain metalinsulator transitions. The theory of quantum computation promises to bring greater computational power over classical computers by making use of some special features of Quantum Mechanics. The first part of this dissertation considers a 3D alloy-type model, where the Hamiltonian is the sum of the finite difference Laplacian corresponding to free motion of an electron and a random potential generated by a sign-indefinite single-site potential. The result shows that localization occurs in the weak disorder regime, i.e., when the coupling parameter λ is very small, for energies E ≤ −Cλ² . The second part of this dissertation considers adiabatic quantum computing (AQC) algorithms for the unstructured search problem to the case when the number of marked items is unknown. In an ideal situation, an explicit quantum algorithm together with a counting subroutine are given that achieve the optimal Grover speedup over classical algorithms, i.e., roughly speaking, reduce O(2n ) to O(2n/2 ), where n is the size of the problem. However, if one considers more realistic settings, the result shows this quantum speedup is achievable only under a very rigid control precision requirement (e.g., exponentially small control error).
Ph. D.
APA, Harvard, Vancouver, ISO, and other styles
4

Björnberg, Jakob Erik. "Graphical representations of Ising and Potts models : Stochastic geometry of the quantum Ising model and the space-time Potts model." Doctoral thesis, KTH, Matematik (Inst.), 2009. http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-11267.

Full text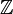
Abstract:
HTML clipboard Statistical physics seeks to explain macroscopic properties of matter in terms of microscopic interactions. Of particular interest is the phenomenon of phase transition: the sudden changes in macroscopic properties as external conditions are varied. Two models in particular are of great interest to mathematicians, namely the Ising model of a magnet and the percolation model of a porous solid. These models in turn are part of the unifying framework of the random-cluster representation, a model for random graphs which was first studied by Fortuin and Kasteleyn in the 1970’s. The random-cluster representation has proved extremely useful in proving important facts about the Ising model and similar models. In this work we study the corresponding graphical framework for two related models. The first model is the transverse field quantum Ising model, an extension of the original Ising model which was introduced by Lieb, Schultz and Mattis in the 1960’s. The second model is the space–time percolation process, which is closely related to the contact model for the spread of disease. In Chapter 2 we define the appropriate space–time random-cluster model and explore a range of useful probabilistic techniques for studying it. The space– time Potts model emerges as a natural generalization of the quantum Ising model. The basic properties of the phase transitions in these models are treated in this chapter, such as the fact that there is at most one unbounded fk-cluster, and the resulting lower bound on the critical value in . In Chapter 3 we develop an alternative graphical representation of the quantum Ising model, called the random-parity representation. This representation is based on the random-current representation of the classical Ising model, and allows us to study in much greater detail the phase transition and critical behaviour. A major aim of this chapter is to prove sharpness of the phase transition in the quantum Ising model—a central issue in the theory— and to establish bounds on some critical exponents. We address these issues by using the random-parity representation to establish certain differential inequalities, integration of which gives the results. In Chapter 4 we explore some consequences and possible extensions of the results established in Chapters 2 and 3. For example, we determine the critical point for the quantum Ising model in 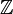and in ‘star-like’ geometries.
HTML clipboard Statistisk fysik syftar till att förklara ett materials makroskopiska egenskaper i termer av dess mikroskopiska struktur. En särskilt intressant egenskap är är fenomenet fasövergång, det vill säga en plötslig förändring i de makroskopiska egenskaperna när externa förutsättningar varieras. Två modeller är särskilt intressanta för en matematiker, nämligen Ising-modellen av en magnet och perkolationsmodellen av ett poröst material. Dessa två modeller sammanförs av den så-kallade fk-modellen, en slumpgrafsmodell som först studerades av Fortuin och Kasteleyn på 1970-talet. fk-modellen har sedermera visat sig vara extremt användbar för att bevisa viktiga resultat om Ising-modellen och liknande modeller. I den här avhandlingen studeras den motsvarande grafiska strukturen hos två näraliggande modeller. Den första av dessa är den kvantteoretiska Isingmodellen med transverst fält, vilken är en utveckling av den klassiska Isingmodellen och först studerades av Lieb, Schultz och Mattis på 1960-talet. Den andra modellen är rumtid-perkolation, som är nära besläktad med kontaktmodellen av infektionsspridning. I Kapitel 2 definieras rumtid-fk-modellen, och flera probabilistiska verktyg utforskas för att studera dess grundläggande egenskaper. Vi möter rumtid-Potts-modellen, som uppenbarar sig som en naturlig generalisering av den kvantteoretiska Ising-modellen. De viktigaste egenskaperna hos fasövergången i dessa modeller behandlas i detta kapitel, exempelvis det faktum att det i fk-modellen finns högst en obegränsad komponent, samt den undre gräns för det kritiska värdet som detta innebär. I Kapitel 3 utvecklas en alternativ grafisk framställning av den kvantteoretiska Ising-modellen, den så-kallade slumpparitetsframställningen. Denna är baserad på slumpflödesframställningen av den klassiska Ising-modellen, och är ett verktyg som låter oss studera fasövergången och gränsbeteendet mycket närmare. Huvudsyftet med detta kapitel är att bevisa att fasövergången är skarp—en central egenskap—samt att fastslå olikheter för vissa kritiska exponenter. Metoden består i att använda slumpparitetsframställningen för att härleda vissa differentialolikheter, vilka sedan kan integreras för att lägga fast att gränsen är skarp. I Kapitel 4 utforskas några konsekvenser, samt möjliga vidareutvecklingar, av resultaten i de tidigare kapitlen. Exempelvis bestäms det kritiska värdet hos den kvantteoretiska Ising-modellen på 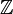, samt i ‘stjärnliknankde’ geometrier.
QC 20100705
APA, Harvard, Vancouver, ISO, and other styles
5

Sugishita, Sotaro. "Construction of a new model generating three-dimensional random volumes:Towards a formulation of membrane theory." 京都大学 (Kyoto University), 2016. http://hdl.handle.net/2433/215308.

Full text
APA, Harvard, Vancouver, ISO, and other styles
6

Charbonnier, Séverin. "Liouville theory and random maps." Thesis, Université Paris-Saclay (ComUE), 2018. http://www.theses.fr/2018SACLS265/document.

Full text
Abstract:
Cette thèse explore divers aspects des cartes aléatoires par l'étude de trois modèles. Dans un premier temps, nous examinons les propriétés d’une mesure définie sur l’ensemble des triangulations de Delaunay planaires comportant n sommets, qui est un modèle de cartes où les arêtes sont décorées par des angles. Nous montrons ainsi que la mesure est égale à la mesure de Weil-Petersson sur l’espace des modules des surfaces de Riemann planaires marquées. Sont aussi montrées deux propriétés de la mesures, premiers pas d'une étude de la limite continue de ce modèle. Dans un deuxième temps, nous définissons des fonctions de corrélations sur les graphes de Strebel planaires isopérimétriques à n faces, qui sont des cartes métriques trivalentes. Les périmètres des faces sont fixés. Nous recourons au théorème de Kontsevich pour calculer les fonctions de corrélations en termes de nombres d’intersection de classes de Chern sur l’espace des modules des surfaces de Riemann. Pour la fonction à une face marquée, la limite des grandes cartes est examinée via l’approximation du point-selle, pour différents régimes du périmètre de la face marquée, et nous déduisons le régime où le comportement de la fonction de corrélation n’est pas trivial. Les fonctions de corrélations peuvent être calculées de manière systématique par la récurrence topologique. Partant, nous calculons la courbe spectrale de notre modèle, ce qui nous permet de montrer qu’il existe une courbe spectrale critique. Nous déduisons de cette courbe critique que la limite continue des graphes de Strebel isopérimétriques est un modèle minimal de type (3,2), habillé par la théorie de Liouville. Cela correspond bien à la gravité pure. Enfin, nous abordons la question des symétries dans le modèle d’Ising sur cartes aléatoires. Certaines fonctions de corrélations de ce modèle comptent le nombre de cartes bicolores avec des faces marquées, les bords, ayant des conditions aux bords mixtes, calculées par récurrence à partir de la courbe spectrale du modèle. Nous prouvons ici que, pour des courbes spectrales génériques, les fonctions de corrélations des cartes à un bord mixte sont symétriques par rotation et par inversion du bord mixte. Nous décrivons ensuite les conséquences de telles symétries, suggérant une possible reformulation du modèle en termes de chaînes de spins
This thesis explore several aspects of random maps through the study of three models. First, we examine the properties of a measure defined on the set of planar Delaunay triangulations with n vertices, a model in which the edges of the maps are decorated with angles. We show that the measure is the Weil-Petersson volume form on the moduli space of planar Riemann surfaces having n marked points. Two other properties, first steps toward the continuous limit study of the model, are also shown. Second, we define correlation functions on isoperimetric planar Strebel graphs with n faces, which are trivalent maps whose edges are decorated by positive lengths, and whose faces have a fixed perimeter. Kontsevich's theorem allows us to compute the correlation functions in terms of the intersection numbers of Chern classes of moduli space of Riemann surfaces. The continuous limit of the one-point function is computed in different regimes for the perimeter of the marked face via the saddle-point approximation. We identify the regime in which the behaviour of the one-point function is not trivial. The correlation functions can be computed in a systematic way by the Topological Recursion. To do so, we compute the spectral curve of the model, and show that there exists a critical spectral curve. We deduce from the latter that the continuous limit of isoperimetric Strebel graphs is a (3,2) minimal model dressed by Liouville theory: it corresponds to pure gravity. Last, we address the problem of symmetries in the Ising model on random maps. Some correlation functions of this model count the bi-colored maps with marked faces having mixed boundary conditions. They are computed via a recursive formula and the spectral curve of the model. We prove here that the correlation functions of maps with one mixed boundary, computed from the recursive relation with generic spectral curve, are invariant under rotation and inversion of the mixed boundary. We describe the consequences of such symmetries, suggesting a possible reformulation of the model in terms of spin chains
APA, Harvard, Vancouver, ISO, and other styles
7

Palaniswamy, Basker. "Improving authentication and key management for intra and inter vehicular communication." Thesis, Queensland University of Technology, 2022. https://eprints.qut.edu.au/236249/1/Basker%2BPalaniswamy%2BThesis.pdf.

Full text
Abstract:
There are two types of vehicular communications: intra-vehicular and inter-vehicular. Widely used intra-vehicular communications protocols include Controller Area Network (CAN) 2.0B and Society of Automotive Engineers (SAE) J1939. Neither CAN 2.0B or SAE J1939 have included security mechanisms to prevent adversarial attacks. Adversaries may modify messages without detection. Inter-vehicular communications includes both vehicle-to-infrastructure and vehicle-to-vehicle communications. These are also vulnerable to attack. Manipulation of vehicular communications can have physical consequences endangering human life. This work aims to address this by analysing existing authentication protocols and designing secure authentication mechanisms for inter-vehicular and intra-vehicular communications to prevent certain adversarial attacks.
APA, Harvard, Vancouver, ISO, and other styles
8

Kuppusamy, Lakshmi Devi. "Modelling client puzzles and denial-of-service resistant protocols." Thesis, Queensland University of Technology, 2012. https://eprints.qut.edu.au/61032/1/Lakshmi_Kuppusamy_Thesis.pdf.

Full text
Abstract:
Denial-of-service (DoS) attacks are a growing concern to networked services like the Internet. In recent years, major Internet e-commerce and government sites have been disabled due to various DoS attacks. A common form of DoS attack is a resource depletion attack, in which an attacker tries to overload the server's resources, such as memory or computational power, rendering the server unable to service honest clients. A promising way to deal with this problem is for a defending server to identify and segregate malicious traffic as earlier as possible. Client puzzles, also known as proofs of work, have been shown to be a promising tool to thwart DoS attacks in network protocols, particularly in authentication protocols. In this thesis, we design efficient client puzzles and propose a stronger security model to analyse client puzzles. We revisit a few key establishment protocols to analyse their DoS resilient properties and strengthen them using existing and novel techniques. Our contributions in the thesis are manifold. We propose an efficient client puzzle that enjoys its security in the standard model under new computational assumptions. Assuming the presence of powerful DoS attackers, we find a weakness in the most recent security model proposed to analyse client puzzles and this study leads us to introduce a better security model for analysing client puzzles. We demonstrate the utility of our new security definitions by including two hash based stronger client puzzles. We also show that using stronger client puzzles any protocol can be converted into a provably secure DoS resilient key exchange protocol. In other contributions, we analyse DoS resilient properties of network protocols such as Just Fast Keying (JFK) and Transport Layer Security (TLS). In the JFK protocol, we identify a new DoS attack by applying Meadows' cost based framework to analyse DoS resilient properties. We also prove that the original security claim of JFK does not hold. Then we combine an existing technique to reduce the server cost and prove that the new variant of JFK achieves perfect forward secrecy (the property not achieved by original JFK protocol) and secure under the original security assumptions of JFK. Finally, we introduce a novel cost shifting technique which reduces the computation cost of the server significantly and employ the technique in the most important network protocol, TLS, to analyse the security of the resultant protocol. We also observe that the cost shifting technique can be incorporated in any Diffine{Hellman based key exchange protocol to reduce the Diffie{Hellman exponential cost of a party by one multiplication and one addition.
APA, Harvard, Vancouver, ISO, and other styles
9

Puschmann, Martin. "Anderson transitions on random Voronoi-Delaunay lattices." Doctoral thesis, Universitätsbibliothek Chemnitz, 2017. http://nbn-resolving.de/urn:nbn:de:bsz:ch1-qucosa-231900.

Full text
Abstract:
The dissertation covers phase transitions in the realm of the Anderson model of localization on topologically disordered Voronoi-Delaunay lattices. The disorder is given by random connections which implies correlations due to the restrictive lattice construction. Strictly speaking, the system features "strong anticorrelation", which is responsible for quenched long-range fluctuations of the coordination number. This attribute leads to violations of universal behavior in various system, e.g. Ising and Potts model, and to modifications of the Harris and the Imry-Ma criteria. In general, these exceptions serve to further understanding of critical phenomena. Hence, the question arises whether such deviations also occur in the realm of the Anderson model of localization in combination with random Voronoi-Delaunay lattice. For this purpose, four cases, which are distinguished by the spatial dimension of the systems and by the presence or absence of a magnetic field, are investigated by means of two different methods, i.e the multifractal analysis and the recursive Green function approach. The behavior is classified by the existence and type of occurring phase transitions and by the critical exponent v of the localization length. The results for the four cases can be summarized as follows. In two-dimensional systems, no phase transitions occur without a magnetic field, and all states are localized as a result of topological disorder. The behavior changes under the influence of the magnetic field. There are so-called quantum Hall transitions, which are phase changes between two localized regions. For low magnetic field strengths, the resulting exponent v ≈ 2.6 coincides with established values in literature. For higher strengths, an increased value, v ≈ 2.9, was determined. The deviations are probably caused by so-called Landau level coupling, where electrons scatter between different Landau levels. In contrast, the principle behavior in three-dimensional systems is equal in both cases. Two localization-delocalization transitions occur in each system. For these transitions the exponents v ≈ 1.58 and v ≈ 1.45 were determined for systems in absence and in presence of a magnetic field, respectively. This behavior and the obtained values agree with known results, and thus no deviation from the universal behavior can be observed
Diese Dissertation behandelt Phasenübergange im Rahmen des Anderson-Modells der Lokalisierung in topologisch ungeordneten Voronoi-Delaunay-Gittern. Die spezielle Art der Unordnung spiegelt sich u.a. in zufälligen Verknüpfungen wider, welche aufgrund der restriktiven Gitterkonstruktion miteinander korrelieren. Genauer gesagt zeigt das System eine "starke Antikorrelation", die dafür sorgt, dass langreichweitige Fluktuationen der Verknüpfungszahl unterdrückt werden. Diese Eigenschaft hat in anderen Systemen, z.B. im Ising- und Potts-Modell, zur Abweichung vom universellen Verhalten von Phasenübergängen geführt und bewirkt eine Modifikation von allgemeinen Aussagen, wie dem Harris- and Imry-Ma-Kriterium. Die Untersuchung solcher Ausnahmen dient zur Weiterentwicklung des Verständnisses von kritischen Phänomenen. Somit stellt sich die Frage, ob solche Abweichungen auch im Anderson-Modell der Lokalisierung unter Verwendung eines solchen Gitters auftreten. Dafür werden insgesamt vier Fälle, welche durch die Dimension des Gitters und durch die An- bzw. Abwesenheit eines magnetischen Feldes unterschieden werden, mit Hilfe zweier unterschiedlicher Methoden, d.h. der Multifraktalanalyse und der rekursiven Greensfunktionsmethode, untersucht. Das Verhalten wird anhand der Existenz und Art der Phasenübergänge und anhand des kritischen Exponenten v der Lokalisierungslänge unterschieden. Für die vier Fälle lassen sich die Ergebnisse wie folgt zusammenfassen. In zweidimensionalen Systemen treten ohne Magnetfeld keine Phasenübergänge auf und alle Zustände sind infolge der topologischen Unordnung lokalisiert. Unter Einfluss des Magnetfeldes ändert sich das Verhalten. Es kommt zur Ausformung von Landau-Bändern mit sogenannten Quanten-Hall-Übergängen, bei denen ein Phasenwechsel zwischen zwei lokalisierten Bereichen auftritt. Für geringe Magnetfeldstärken stimmen die erzielten Ergebnisse mit den bekannten Exponenten v ≈ 2.6 überein. Allerdings wurde für stärkere magnetische Felder ein höherer Wert, v ≈ 2.9, ermittelt. Die Abweichungen gehen vermutlich auf die zugleich gestiegene Unordnungsstärke zurück, welche dafür sorgt, dass Elektronen zwischen verschiedenen Landau-Bändern streuen können und so nicht das kritische Verhalten eines reinen Quanten-Hall-Überganges repräsentieren. Im Gegensatz dazu ist das Verhalten in dreidimensionalen Systemen für beide Fälle ähnlich. Es treten in jedem System zwei Phasenübergänge zwischen lokalisierten und delokalisierten Bereichen auf. Für diese Übergänge wurde der Exponent v ≈ 1.58 ohne und v ≈ 1.45 unter Einfluss eines magnetischen Feldes ermittelt. Dieses Verhalten und die jeweils ermittelten Werte stimmen mit bekannten Ergebnissen überein. Eine Abweichung vom universellen Verhalten wird somit nicht beobachtet
APA, Harvard, Vancouver, ISO, and other styles
10

Lippold, Georg. "Encryption schemes and key exchange protocols in the certificateless setting." Thesis, Queensland University of Technology, 2010. https://eprints.qut.edu.au/41697/1/Georg_Lippold_Thesis.pdf.

Full text
Abstract:
The contributions of this thesis fall into three areas of certificateless cryptography. The first area is encryption, where we propose new constructions for both identity-based and certificateless cryptography. We construct an n-out-of- n group encryption scheme for identity-based cryptography that does not require any special means to generate the keys of the trusted authorities that are participating. We also introduce a new security definition for chosen ciphertext secure multi-key encryption. We prove that our construction is secure as long as at least one authority is uncompromised, and show that the existing constructions for chosen ciphertext security from identity-based encryption also hold in the group encryption case. We then consider certificateless encryption as the special case of 2-out-of-2 group encryption and give constructions for highly efficient certificateless schemes in the standard model. Among these is the first construction of a lattice-based certificateless encryption scheme. Our next contribution is a highly efficient certificateless key encapsulation mechanism (KEM), that we prove secure in the standard model. We introduce a new way of proving the security of certificateless schemes based that are based on identity-based schemes. We leave the identity-based part of the proof intact, and just extend it to cover the part that is introduced by the certificateless scheme. We show that our construction is more efficient than any instanciation of generic constructions for certificateless key encapsulation in the standard model. The third area where the thesis contributes to the advancement of certificateless cryptography is key agreement. Swanson showed that many certificateless key agreement schemes are insecure if considered in a reasonable security model. We propose the first provably secure certificateless key agreement schemes in the strongest model for certificateless key agreement. We extend Swanson's definition for certificateless key agreement and give more power to the adversary. Our new schemes are secure as long as each party has at least one uncompromised secret. Our first construction is in the random oracle model and gives the adversary slightly more capabilities than our second construction in the standard model. Interestingly, our standard model construction is as efficient as the random oracle model construction.
APA, Harvard, Vancouver, ISO, and other styles
More sources

Books on the topic "Quantum random oracle model"

1

Glazer, Victor. Some results concerning security in the Random Oracle Model. 2005.

Find full text
APA, Harvard, Vancouver, ISO, and other styles
2

Horing, Norman J. Morgenstern. Random Phase Approximation Plasma Phenomenology, Semiclassical and Hydrodynamic Models; Electrodynamics. Oxford University Press, 2018. http://dx.doi.org/10.1093/oso/9780198791942.003.0010.

Full text
Abstract:
Chapter 10 reviews both homogeneous and inhomogeneous quantum plasma dielectric response phenomenology starting with the RPA polarizability ring diagram in terms of thermal Green’s functions, also energy eigenfunctions. The homogeneous dynamic, non-local inverse dielectric screening functions (K) are exhibited for 3D, 2D, and 1D, encompassing the non-local plasmon spectra and static shielding (e.g. Friedel oscillations and Debye-Thomas-Fermi shielding). The role of a quantizing magnetic field in K is reviewed. Analytically simpler models are described: the semiclassical and classical limits and the hydrodynamic model, including surface plasmons. Exchange and correlation energies are discussed. The van der Waals interaction of two neutral polarizable systems (e.g. physisorption) is described by their individual two-particle Green’s functions: It devolves upon the role of the dynamic, non-local plasma image potential due to screening. The inverse dielectric screening function K also plays a central role in energy loss spectroscopy. Chapter 10 introduces electromagnetic dyadic Green’s functions and the inverse dielectric tensor; also the RPA dynamic, non-local conductivity tensor with application to a planar quantum well. Kramers–Krönig relations are discussed. Determination of electromagnetic response of a compound nanostructure system having several nanostructured parts is discussed, with applications to a quantum well in bulk plasma and also to a superlattice, resulting in coupled plasmon spectra and polaritons.
APA, Harvard, Vancouver, ISO, and other styles

Book chapters on the topic "Quantum random oracle model"

1

Alamati, Navid, Varun Maram, and Daniel Masny. "Non-Observable Quantum Random Oracle Model." In Post-Quantum Cryptography, 417–44. Cham: Springer Nature Switzerland, 2023. http://dx.doi.org/10.1007/978-3-031-40003-2_16.

Full text
APA, Harvard, Vancouver, ISO, and other styles
2

Alkim, Erdem, Nina Bindel, Johannes Buchmann, Özgür Dagdelen, Edward Eaton, Gus Gutoski, Juliane Krämer, and Filip Pawlega. "Revisiting TESLA in the Quantum Random Oracle Model." In Post-Quantum Cryptography, 143–62. Cham: Springer International Publishing, 2017. http://dx.doi.org/10.1007/978-3-319-59879-6_9.

Full text
APA, Harvard, Vancouver, ISO, and other styles
3

Hhan, Minki, Keita Xagawa, and Takashi Yamakawa. "Quantum Random Oracle Model with Auxiliary Input." In Lecture Notes in Computer Science, 584–614. Cham: Springer International Publishing, 2019. http://dx.doi.org/10.1007/978-3-030-34578-5_21.

Full text
APA, Harvard, Vancouver, ISO, and other styles
4

Zhang, Jiayu. "Delegating Quantum Computation in the Quantum Random Oracle Model." In Theory of Cryptography, 30–60. Cham: Springer International Publishing, 2019. http://dx.doi.org/10.1007/978-3-030-36033-7_2.

Full text
APA, Harvard, Vancouver, ISO, and other styles
5

Shang, Tao, and Jianwei Liu. "Security Analysis Based on Quantum Random Oracle Model." In Secure Quantum Network Coding Theory, 213–39. Singapore: Springer Singapore, 2020. http://dx.doi.org/10.1007/978-981-15-3386-0_11.

Full text
APA, Harvard, Vancouver, ISO, and other styles
6

Chiesa, Alessandro, Peter Manohar, and Nicholas Spooner. "Succinct Arguments in the Quantum Random Oracle Model." In Theory of Cryptography, 1–29. Cham: Springer International Publishing, 2019. http://dx.doi.org/10.1007/978-3-030-36033-7_1.

Full text
APA, Harvard, Vancouver, ISO, and other styles
7

Feng, Hanwen, Jianwei Liu, and Qianhong Wu. "Secure Stern Signatures in Quantum Random Oracle Model." In Lecture Notes in Computer Science, 425–44. Cham: Springer International Publishing, 2019. http://dx.doi.org/10.1007/978-3-030-30215-3_21.

Full text
APA, Harvard, Vancouver, ISO, and other styles
8

Unruh, Dominique. "Quantum Position Verification in the Random Oracle Model." In Advances in Cryptology – CRYPTO 2014, 1–18. Berlin, Heidelberg: Springer Berlin Heidelberg, 2014. http://dx.doi.org/10.1007/978-3-662-44381-1_1.

Full text
APA, Harvard, Vancouver, ISO, and other styles
9

Don, Jelle, Serge Fehr, Christian Majenz, and Christian Schaffner. "Online-Extractability in the Quantum Random-Oracle Model." In Advances in Cryptology – EUROCRYPT 2022, 677–706. Cham: Springer International Publishing, 2022. http://dx.doi.org/10.1007/978-3-031-07082-2_24.

Full text
APA, Harvard, Vancouver, ISO, and other styles
10

Liu, Qipeng. "Non-uniformity and Quantum Advice in the Quantum Random Oracle Model." In Advances in Cryptology – EUROCRYPT 2023, 117–43. Cham: Springer Nature Switzerland, 2023. http://dx.doi.org/10.1007/978-3-031-30545-0_5.

Full text
APA, Harvard, Vancouver, ISO, and other styles

Conference papers on the topic "Quantum random oracle model"

1

Guha, Aishi, Noah A. Davis, and Brian R. La Cour. "Classical Attack on Bell Inequalities." In Quantum 2.0, QTh3A.7. Washington, D.C.: Optica Publishing Group, 2024. http://dx.doi.org/10.1364/quantum.2024.qth3a.7.

Full text
Abstract:
Representing multi-mode squeezed light with a Gaussian random vector, our locally deterministic detection model challenges the CHSH game, achieving fidelities exceeding 96%. Squeezing strength, detector threshold, and efficiency influence the security of the quantum bound.
APA, Harvard, Vancouver, ISO, and other styles
2

Arora, Atul Singh, Andrea Coladangelo, Matthew Coudron, Alexandru Gheorghiu, Uttam Singh, and Hendrik Waldner. "Quantum Depth in the Random Oracle Model." In STOC '23: 55th Annual ACM Symposium on Theory of Computing. New York, NY, USA: ACM, 2023. http://dx.doi.org/10.1145/3564246.3585153.

Full text
APA, Harvard, Vancouver, ISO, and other styles
3

Zhang, Zhen, Huiyan Chen, and Yufan Chen. "A provable secure signature in the quantum random oracle model." In 2022 International Conference on Blockchain Technology and Information Security (ICBCTIS). IEEE, 2022. http://dx.doi.org/10.1109/icbctis55569.2022.00021.

Full text
APA, Harvard, Vancouver, ISO, and other styles
4

Abla, Parhat. "Lattice Based Group Key Exchange Protocol in the Standard Model." In 2nd International Conference on Machine Learning &Trends (MLT 2021). AIRCC Publishing Corporation, 2021. http://dx.doi.org/10.5121/csit.2021.111113.

Full text
Abstract:
Group key exchange schemes allow group members to agree on a session key. Although there are many works on constructing group key exchange schemes, but most of them are based on algebraic problems which can be solved by quantum algorithms in polynomial time. Even if several works considered lattice based group key exchange schemes, believed to be post-quantum secure, but only in the random oracle model. In this work, we propose a group key exchange scheme based on ring learning with errors problem. On contrast to existing schemes, our scheme is proved to be secure in the standard model. To achieve this, we define and instantiate multi-party key reconciliation mechanism. Furthermore, using known compiler with lattice based signature schemes, we can achieve authenticated group key exchange with postquantum security.
APA, Harvard, Vancouver, ISO, and other styles
5

Zhang, Jiayu. "Succinct blind Quantum computation using a random oracle." In STOC '21: 53rd Annual ACM SIGACT Symposium on Theory of Computing. New York, NY, USA: ACM, 2021. http://dx.doi.org/10.1145/3406325.3451082.

Full text
APA, Harvard, Vancouver, ISO, and other styles
6

Tang, Guangming, and Jing Liu. "A Random Oracle Model for Information Hiding Resisting Extracting." In 2009 International Conference on E-Business and Information System Security (EBISS). IEEE, 2009. http://dx.doi.org/10.1109/ebiss.2009.5137892.

Full text
APA, Harvard, Vancouver, ISO, and other styles
7

Wang, Xu An, Jianfeng Ma, and Xiaoyuan Yang. "New Compact CCA Secure Elgamal Scheme in the Random Oracle Model." In 2015 International Conference on Intelligent Networking and Collaborative Systems (INCOS). IEEE, 2015. http://dx.doi.org/10.1109/incos.2015.41.

Full text
APA, Harvard, Vancouver, ISO, and other styles
8

Holenstein, Thomas, Robin Künzler, and Stefano Tessaro. "The equivalence of the random oracle model and the ideal cipher model, revisited." In the 43rd annual ACM symposium. New York, New York, USA: ACM Press, 2011. http://dx.doi.org/10.1145/1993636.1993650.

Full text
APA, Harvard, Vancouver, ISO, and other styles
9

Chen, Jianhong. "Identity-Based Parallel Key-Insulated Proxy Signature in the Random Oracle Model." In 2020 International Conference on E-Commerce and Internet Technology (ECIT). IEEE, 2020. http://dx.doi.org/10.1109/ecit50008.2020.00070.

Full text
APA, Harvard, Vancouver, ISO, and other styles
10

Courant, Judicaël, Marion Daubignard, Cristian Ene, Pascal Lafourcade, and Yassine Lakhnech. "Towards automated proofs for asymmetric encryption schemes in the random oracle model." In the 15th ACM conference. New York, New York, USA: ACM Press, 2008. http://dx.doi.org/10.1145/1455770.1455817.

Full text
APA, Harvard, Vancouver, ISO, and other styles
You might also be interested in the extended bibliographies on the topic 'Quantum random oracle model' for particular source types:
Journal articles Dissertations / Theses
We offer discounts on all premium plans for authors whose works are included in thematic literature selections. Contact us to get a unique promo code!

To the bibliography